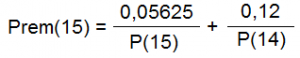2.3. Probabilidad Apostada

Introducción

El concepto de probabilidad ya lo hemos definido con anterioridad y es básico para seguir este artículo. Entre otras cosas, explicamos la ley de Laplace que nos dice que la probabilidad de un suceso es el número de casos favorables dividido por el número de casos posibles y pusimos el ejemplo de la moneda donde tenemos un 50% de probabilidad de acertar cara o cruz.

También hemos hablado de la probabilidad real o natural de que salga un signo en un partido de fútbol.

Lo que vemos en la imagen es el reverso de un décimo de Lotería Nacional. Al ser un décimo, los premios debemos dividirlos entre 10 porque no hemos comprado el billete completo.

En él vemos que si acertamos 5 números, nos toca 100.000 euros (25.000 o 5.000 según si es el primer, segundo o tercer premio). Y da igual que el décimo lo tengas tú solo, que lo haya comprado otras personas o que toda tu familia o grupo de amigos juguéis el mismo número, sabes lo que te toca según lo que aciertes.

Premios en La Quiniela

Pero… ¿cuánto te toca si aciertas un 14 en La Quiniela? No es tan fácil de saber, ¿verdad? Porque para el premio de 14 está destinado el 16% de la recaudación y el importe se dividirá entre todos los acertanes de esa jornada.

Aquí no da igual que yo tenga 14 y mi vecino también. Porque si ha habido 5.000.000€ de recaudación y soy el único acertante de 14 cobraré 800.000€, pero como haya otro que también lo acierte cobraré 400.000€, y como seamos 12 pasará ligeramente de los 66.666 euros.

Me interesa por lo tanto, acertar, pero acertar yo solo.

No puedo sellar una combinación y vetar esas columnas para que nadie más las pueda sellar. Pero lo que sí que puedo hacer es saber qué están apostando los demás para no apostarlo yo. ¿Cómo? Entremos en materia.

Probabilidad Apostada

Para iniciarnos de la manera más sencilla posible, vamos a poner un ejemplo. Supongamos que somos 4 personas y que vamos a jugar a adivinar si sale cara o cruz en una moneda.

Normas:

• Participar cuesta 1€,
• el 50% de la recaudación se lo queda la banca por organizar el juego y
• el otro 50% se reparte entre los que acierten.

Siendo 4, se colocan 4 euros y se destinan 2€ a premios. Toca apostar y supongamos que se dan estas apuestas:

• Jugador A: Cara.
• Jugador B: Cara
• Jugador C: Cara

Tú: ¿Qué apostarías?

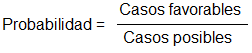
Sin embargo, vemos que si sale Cara, la cantidad destinada a premios (2€) la vamos a tener que repartir entre todos los ganadores, que de momento ya son 3.

En este momento, la probabilidad apostada de que salga cara es de 3/4 (tres personas apuestan cara de las cuatro posibles) = 75%. Si saliera Cara, los tres acertantes se repartirían el premio de 2€, y les tocaría a cada uno 0,67€. Acertando pierden dinero.

Si apuesto Cruz y sale, sería único acertante y los 2€ serían íntegros para mí. La probabiliad apostada sería de 1 (yo) dividido entre 4 (todos los que apostamos) = 25%.

La probabilidad apostada cambia cada vez que se reinicia la apuesta.

Ahora supongamos que las apuestas son privadas, que cada participante apunta en un papel su nombre y su apuesta «cara» o «cruz» y lo mete en un bote. Apuestan los tres jugadores y te toca a ti. ¿Qué apostarías?

Yo, intentaría saber qué han apostado los demás para inclinarme por la opción menos apostada si la hay. Si no la hay, no apostaría.

En La Quiniela, todas las semanas hay columnas muy fáciles que se sobreapuestan y, otras que no se apuestan o se apuestan poco siendo igualmente probables. Se trata de apostar por la opción que tiene menos probabilidad apostada que real.

Probabilidad apostada del 14 premiado

La probabilidad apostada del 14 premiado se puede calcular fácilmente una vez conocido el escrutinio, ya que tenemos los datos necesarios: los casos favorables son los acertantes que ha habido de 14 y los casos posibles, son todas las columnas que se validan.

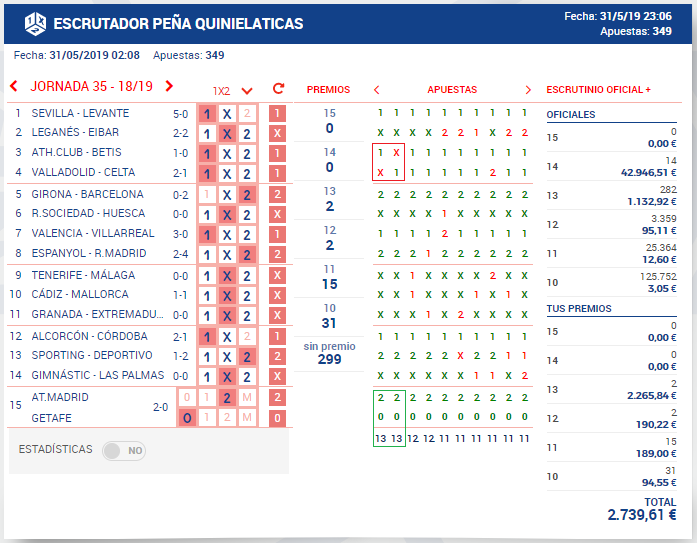
Por ejemplo, en la jornada 35 de la temporada 2018/2019 se recaudó 4.259.775,00€, que corresponden a 5.679.700 columnas (precio por columna en el momento de escribir este artículo = 0,75€) y hubieron 14 acertanes de 14.

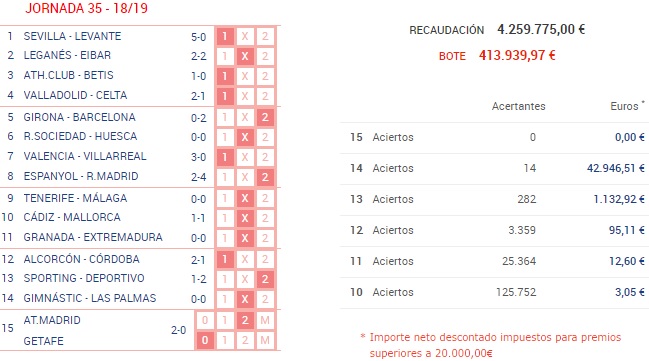
Si hacemos el cálculo:

P(14) = AC(14) / Apuestas

P. apostada del 14 de la j.35 = 14/5.679.700 = 0,00000246 = 2,46E-06

Ese 2,46E-06 es la probabilidad apostada de esa columna que estaba repetida 14 veces en el total de las columnas validadas. Cuanto más repetida esté una columna, mayor probabilidad apostada tendrá y menor premio le corresponderá en el caso de salir.

Por cierto, en esta jornada, obtuvimos 2 treces en la Peña Quinielaticas y teníamos el pleno al 15 acertado. Si hubiera empatado el Betis o el Celta, se estimaba que teníamos 15 único. 

Cuando no aparecen acertantes de 14 y se genera bote es porque nadie ha apostado esa columna y por lo tanto tiene una probabilidad apostada cero. Por ejemplo, la jornada 50 del mismo año 2018-2019.

Prob. apostada j.50 = 0/5.111.511=0

En esa jornada 50, también tuvimos 13 aciertos en la Peña Quinielaticas. Fallamos el Deportivo-Rayo MJ que teníamos en esa columna un 1 y salió 2.

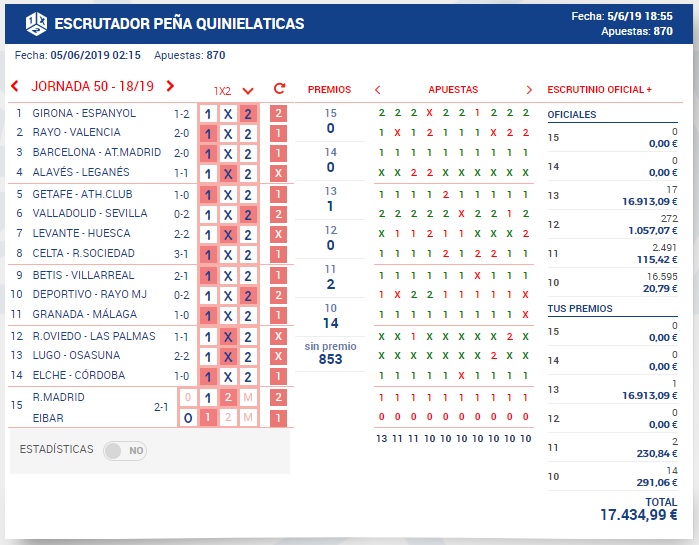
Si sumamos las probabilidades de todas las columnas apostadas, el resultado es 1.

El premio no depende de la recaudación

Que la recaudación de La Quiniela ha descendido mucho durante los años, es un hecho evidente. 

Sin embargo, al contrario de lo que mucha gente piensa, el premio no depende de la recaudación. Es decir, a menor recaudación los premios no tienen por qué ser menores. Vamos a demostrarlo:

• Acabamos de ver que P(14) = AC(14) / Apuestas
• Las apuestas se conocen por la recaudación. Apuestas = Recaudación / 0,75
• Si sustituimos «Apuestas» en la primera fórmula se nos quedaría así:

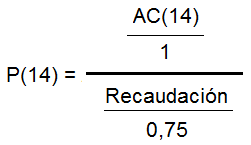
• Despejando los acertantes «AC(14)» quedaría:

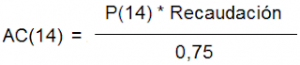
• Por otro lado sabemos que el premio que recibe el acertante de 14 según las normas de LAE en el momento la escritura de este artículo (junio 2019) es el 16% de la recaudación dividido por el número de acertantes:

• Sustituyendo AC(14) por la fórmula anterior, queda:

• Ahora podemos eliminar «Recaudación»

• Y finalmente aplicamos la ley de extremos y medios:

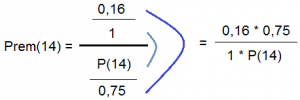
• Y por lo tanto:

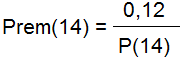
• Conclusión: el producto de la probabilidad apostada del 14 premiado por el premio del 14 es constante y vale 0,12.

¿Y esto qué quiere decir exactamente?

Pues lo que decíamos al principio de este apartado que el premio no depende de la recaudación, lo hemos eliminamos de la fórmula. Así que los que dicen que al bajar la recaudación bajan los premios, sencillamente se equivocan. De la recaudación depende el número de acertantes, a mayor recaudación más acertantes.

El premio de 14 aciertos únicamente depende de 3 factores:

1. La probabilidad apostada «P(14)»
2. El porcentaje destinado a premios de la recaudación: 16% o 0,16 que aparece en la fórmula.
3. Del precio de la apuesta: 0,75 que también aparece en la fórmula.

Volviendo a la fórmula anterior, vemos que cada probabilidad tiene su premio asociado y viceversa. Es decir:

• Sabiendo la probabilidad apostada de cada columna, se puede calcular lo que va a cobrar.
• Y conociendo el premio que se lleva el 14 se sabe su probabilidad apostada sin necesidad de conocer la recaudación.

Probabilidad y premio

La gráfica que representa la relación entre el premio y la probabilidad apostada del 14 es una hipérbola. Para valores muy altos de probabilidad salen premios muy bajos.

A medida que se baja en probabilidad el valor del premio va subiendo gradualmente, primero muy despacio y poco a poco va acelerando la subida hasta que llega a dispararse de manera que donde están las columnas muy poco probables, un pequeño incremento de dificultad incrementa mucho el premio.

El premio crece de manera exponencial con la dificultad, detalle fundamental para comprender la estructura de la quiniela.

Pleno al 15

Teniendo en cuenta que el pleno al 15 se lleva el 7,5% de la recaudación y que el acertante de 15 cobra también un premio de 14, la fórmula para calcular lo que cobra el premio del pleno al 15 en total sería:

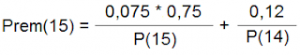
Y por lo tanto: