Agradecimientos
Prácticamente la integridad de mis conocimientos matemático-quinielísticos, pero sobre todo lo que empieza en esta sección de probabilidad, se remonta al año 2003, concretamente un sábado 8 de noviembre cuando Francisco Hernández Hernández habla por primera vez en la historia de La Quiniela sobre que hay dos probabilidades, la apostada y la real. Lo hace con un estudio propio y con sus horas, muchas horas de trabajo y dedicación. Además, presenta también por primera vez la relación entre los logaritmos neperianos aplicados a este juego del 1X2.
Lo hizo en el foro1x2 y ese día debería estar en los libros de historia matemática, pues es el día en el que empezó su divulgación altruista sobre sus conocimientos y su trabajo que se iniciaría por los años 60. Más de un lector, y yo mismo, no habíamos ni nacido. PacoHH, como él mismo se hace llamar en los foros, nació en junio de 1952. Puedes hacerte una idea de lo joven que empezó a ser un quinielista autodidacta.
Francisco Hernández Hernández es el René Descartes de nuestra época. Su blog quinielandia, inaugurado el 16 de junio de 2008 es el mejor manual de instrucciones sobre probabilidad, combinatoria y resto de temas matemáticos relacionados con la quiniela. Desde entonces, muchos posts, blogs e incluso libros se han escrito hablando de probabilidad y esperanza matemática. Todos ellos, estoy seguro, han leído a este señor.
Con Quinielaticas pretendo ordenar todos esos apuntes que inundan carpetas de mi escritorio y redactar, de la manera más ordenada y simple, aquellos conceptos que a priori asustan a muchos por sus nombres técnicos. Espero que los textos que vaya escribiendo de aquí en adelante sean tan útiles como lo fueron para mí y se conviertan en una guía imprescindible para sellar tus apuestas.
Probabilidad
Los lectores de estos artículos entrarán en esta sección con la intención de aprender, comprobar o refrescar conceptos matemáticos aplicados a La Quiniela, y no únicamente conceptos matemáticos. Por ello, aunque sobre probabilidad se puede hablar mucho, aquí me centraré en hablar de probabilidad aplicada al 1X2, saltándome muchos puntos de la teoría de la probabilidad que no considero importantes.
Para empezar diré que las condiciones de signo vistas en el capítulo 1, son muy poco precisas. Ahora hablaremos con números. La probabilidad es un dato mucho más preciso que el signo «1», «X» o «2» que por ellos mismos no dicen nada.
Así, si cogemos un libro de probabilidad y depuramos todo aquello que no nos interesa, la primera página quedaría de esta manera:
Existen experimentos deterministas y aleatorios:
- Soltar una piedra en el agua y esperar a que se hunda es un experimento determinista porque se sabe lo que va a suceder.
- Por el contrario, el resultado de lanzar una moneda al aire o el número de la lotería son sucesos aleatorios.
El resultado de un partido de fútbol también es un suceso aleatorio.
Concepto
La probabilidad, que se denota con la letra P, es la rama de las matemáticas que estudia los sucesos aleatorios. Es la medida de la incertidumbre, el cálculo de las posibilidades que existen de que un suceso se cumpla.
Axiomas de Kolmogórov (1903-1987)
Kolmogórov fue un matemático soviético que hizo progresos importantes en los campos de la teoría de la probabilidad y formuló en 1993 su sistema axiomático a partir de la teoría de conjuntos.
En nuestro ámbito, es como si Kolmogórov nombrara “conjunto” a un partido y “sucesos” a los distintos resultados (signos: 1, X o 2) de ese partido.
Axioma 1: La probabilidad de un suceso cualquiera es un número real que va entre el 0 y el 1, siendo 0 nada probable y 1 un suceso seguro.
En un partido de fútbol tenemos 3 sucesos posibles. El 1, la X y el 2. Cada uno con una probabilidad que va de 0 a 1. Ejemplo:
P(1): 0,45
P(X): 0,29
P(2): 0,26
Axioma 2: La probabilidad total del conjunto es igual a 1.
Es decir, el partido terminará seguro. Sin importar el resultado que se dé.
P(partido): 1
Axioma 3: Se puede calcular la probabilidad de que ocurra alguno de dos sucesos excluyentes, sumando sus probabilidades.
La probabilidad de que el partido que estamos viendo de ejemplo acaben en 1 o X es la suma de sus probabilidades.
P(1X) = P(1) + P(X)
P(1X) = 0,45 + 0,29
P(1X) = 0,74
Teorema o regla de la multiplicación
Esta regla establece que la probabilidad de que ocurran dos o más acontecimientos independientes, es igual al producto de sus probabilidades individuales.
Es decir, supongamos que la probabilidad de que en un boleto de 14 partidos salgan:
A: [de 5 a 10 “unos”] es de 0,70 (70%)
Y la probabilidad de que salgan:
B: [de 2 a 6 “doses”] es de 0,80, (80%)
La probabilidad de que ocurran las dos cosas a la vez es de:
P(AyB) = 0,70*0,80=0,56 (56%)
A mí, particularmente, me gusta expresarme en porcentajes, siendo 0 = 0% y 1 = 100% aunque algunas teorías digan que así no se hace. Me parece muy clarificador a la hora de presentar los datos.
Ley de Laplace
Muchos ejemplos que utilizaremos para explicar aspectos de la probabilidad, se basan en sucesos equiprobables, es decir, que tienen la misma probabilidad de salir.
La ley de Laplace dice que la probabilidad de un suceso es el número de casos favorables dividido por el número de casos posibles.
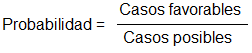
El ejemplo más sencillo es el de acertar si sale cara o cruz al lanzar una moneda. Casos favorables de que salga cara = 1; casos posibles = 2 (cara y cruz).
Probabilidad de acertar que sale cara = 1/2 = 0,5 = 50%.
Esto significa que si lanzáramos 10.000 veces la moneda, 5.000 saldrían cara y otras 5.000 saldrían cruz.
Podéis comprobarlo, aunque ya lo hizo John Kerrich al quedar atrapado en Dinamarca tras la ocupación Nazi en la II Guerra Mundial. Realmente los resultados fueron 5.067 caras (50,67%) y 4.933 cruces (49,33%). Si hubiera seguido tirando, esa diferencia sería cada vez menor, pero imagino que a Kerrich le bastó con 10.000 lanzamientos.
La probabilidad de la columna ganadora
En La Quiniela, cuando se publica el escrutinio, tenemos estos datos. Los casos favorables sería el número de acertantes de 14; y los casos posibles el número de columnas apostadas en total. La probabilidad del 14 premiado se calcula dividiendo el número de acertantes entre las columnas apostadas (que publica LAE al cierre de la validación).
Por ejemplo, en la temporada 16/17 jornada 40, hubo 26 acertantes de 14 y se validaron 6.590.763 apuestas. 26/6.590.763 = 0,00000394 que es la probabilidad de la columna ganadora, en este caso la: 2111X12X2212X2.